FAIR Lessons of the Amtrak Accident

FAIR can be extended to the analysis of risk scenarios that have multiple impact variables, such as in public safety.  This note reports lessons learned from a simple model inspired by the Amtrak crash.

Introduction

The crash of an Amtrak passenger train in Philadelphia (5/13/15), which killed 8 and injured over 200, offers an opportunity to analyze the risk of such situations and consider the investment case for positive train control.  According to NTS Board member Robert Sumwalt PTC “would have prevented the accident if it was operational.” 

Despite “information” in its name, FAIR is a useful and appropriate tool for analyzing many kinds of risk other than information risk.  Let us take this opportunity to apply it to transportation safety.

FAIR has a big drawback, at least as it is typically used.  The result of a FAIR analysis is an estimate of annual loss expectancy (ALE), which is presumed to be measurable on one dimension, inevitably money.  But when matters of public safety are involved, as with transportation and health care, money is only one consideration.  Loss of life, injury, and long-term impairment of quality of life (which together I call life safety) are outcomes that cannot be adequately expressed in money terms, for reasons emotional, philosophical, and political.  Therefore any risk analysis of a transportation or health care scenario must include life safety in addition to financial loss.

One way to assess risk in such a multidimensional outcome scenario is to do a FAIR analysis of each outcome variable separately.  The deliverables to the decision maker is then (1) the ALE for financial loss (2) the ALE for life safety loss and (3) some depiction of how the two ALEs correlate.  It is then up to the decision maker to process these analytical results and set priorities for investment, just as in the case of a purely financial impact the decision maker must decide which of two ALEs is preferable, or whether the investment needed to move from one ALE to another is justified. 

In this note I report on the experience of such a modeling effort, inspired by the Amtrak accident.   I find some interesting and useful insights from using FAIR in this way.

Model Structure

I constructed two simple and nearly parallel FAIR risk analyses of a passenger train risk scenario similar to the May 13 2015 Amtrak crash in Philadelphia.  The main goal of the analysis was to test the ability of the FAIR ontology to support the analysis of a risk scenario having two important impact variables, financial loss and life safety.  This goal makes little demand for representational accuracy of the actual train crash scenario, so the model is simple.  Each impact variable, financial loss (ALE) and life safety loss (expressed as ALE of lives lost), was analyzed using the FAIR ontology.  The two analyses are nearly independent, having only the threat event frequency and the probability distribution of lives lost as a common driver, and in that sense are “nearly parallel.”  The model structure is shown in the following figure.  Lives lost drives fines and judgments as well as being a thing of value in its own right.

Figure 1.  Structure of a FAIR Model with Two Impact Variables.

I used what I considered to be plausible values for parameters of the probability distributions, all of which were of the PERT family.  I do not believe the main lessons of the analysis depend in any meaningful way on the values of the parameters, so I omit discussion of the choices of parameter values.  Likewise the model could easily be built out in considerably more detail without materially changing the results.  Monte Carlo simulation with 1,000 trials was used to model the effect of the several random variables. 

Results

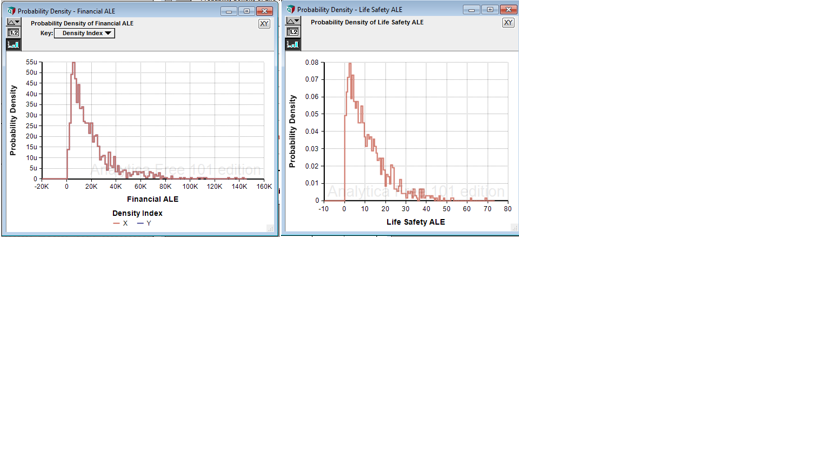
The next two figures show the simulation results for the probability distributions of annual loss expectancies for financial loss and life safety (i.e., lives lost).  (Note that financial loss is measured in $K, so the abscissa for financial ALE is actually $M.)

Figures 2a and 2b.  Financial and Life Safety ALE

The decision maker has one budget to allocate to mitigate both risks, so a very pressing question is whether, and to what degree, mitigating one also mitigates the other.  Do they vary together or opposite to each other?  The next chart is a scatter plot of the simulation results.  Each dot is one MC trial.

Figure 3.  Scatterplot of Financial and Life Safety ALEs.  Each dot is a simulation trial.

Not surprisingly, financial loss and life safety are highly correlated.  This makes intuitive sense since each life lost imposes a risk of lawsuits and settlement costs on the railroad.  However the degree of correlation becomes weaker at higher levels of loss.  If there is any good news for the railroad, it is that spending money to reduce financial loss also tends to reduce life safety loss.

The Counterfactual Scenario

The reason that financial ALE and life safety ALE are so strongly correlated is the high value I put on a lost life (PERT with minimum, most likely, and maximum of $500K, $1000K, $5000K per life).  To test how strongly life safety loss drives financial loss, I constructed a counterfactual model which puts the financial loss of a lost life at zero.  In this structure the connection from Secondary Financial Loss Magnitude to Financial ALE was simply removed.

Figure 4.   Counterfactual Model.  The railroad has no liability for lives lost.

The correlation between the two impact variables now looks like this:

Figure 5.  Scatterplot of Financial and Life Safety ALEs when the railroad has no liability for lives lost.

The correlation is still positive because the worse the accident, the more lives lost and the more equipment destroyed, but looser. 

Conclusions

1.       FAIR can be used, quite straightforwardly, to analyze the risk of scenarios that have multiple impact variables.  What needs to be added is some analysis of how the various loss expectancies relate to each other.  Tradeoffs among ALEs of multiple impact variables is left to the decision maker, or to another analysis.

2.       Making the railroad (or in general the provider) liable for non-financial losses imposed on secondary stakeholders tends to align multiple risk measures in the decision making of the provider.  The greater the liability to the provider, the better the alignment.  This is obvious but the model illuminates the degree to which, and the manner in which, the alignment is created

3.       Therefore modeling of this sort can be useful for public policy analysis.  It could be used to explore different kinds of transfer of liability from secondary stakeholders to the primary stakeholder, and different levels of absolute liability (e.g. should there be limits on the valuation of a life, and what might they be?)

4.       This kind of multi-impact risk analysis can be useful in many kinds of public policy analysis involving risk other than transportation safety, such as health care, pollution, water allocation, earthquake and extreme storm hazard mitigation, and defense planning.